Science Corner: Traveling on the Level

When we last visited the Quandary Den, we saw how our players could take an adaptive path to complexity. By complexity, I mean that the solution to the challenge of the room involved multiple players making distinct and essential contributions. We saw that they were essential by looking at the last-on-the-bus (LOTB) score which looks at the difference between the team’s result with that player and without. If a player has a LOTB score of zero, then their contributions are not essential; they might score one or more points but when they are not there someone else is capable of scoring them. And I say the path to that complexity was adaptive because the experiment started with random actions and applied positive selection whenever mutations added players or actions that contributed to a solution. Then I asked whether other pathways to complexity were possible and provided a simulation for answering that question.

To see whether there is another path to complexity, I modified the simulation so that gene duplication didn’t begin until a complete solution to the room was found by a single player. In that case, fitness has already been maximized and there are no mutations that can increase it. Likewise, adding players cannot add to the fitness either. So at that point, a gene duplication can only either be detrimental (by adding a player who contributes to a loss of health by taking a tag/zap or tagging/zapping a teammate) or neutral. If the new gene is detrimental, it will be removed by negative selection. But what happens to the neutral genes?

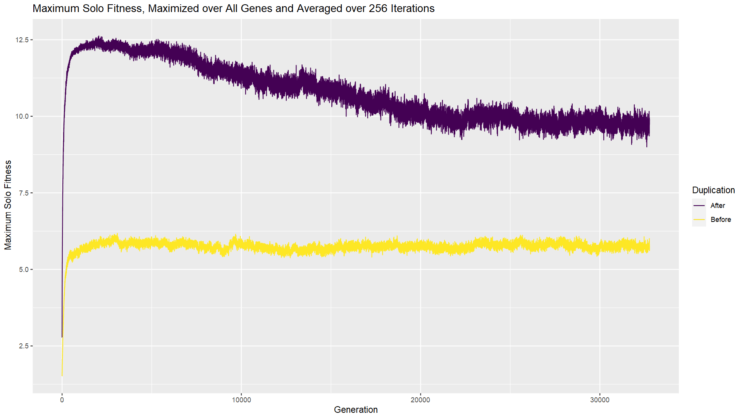
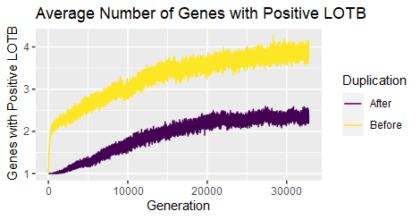
If you had a chance to try the experiment, you likely saw that additional genes do wind up sticking around. What’s more, over time they become essential, as evidenced by the fact that the first gene can no longer solve the room by itself (chart immediately above) and multiple genes have a positive/nonzero LOTB score (chart at top of post). How does that happen when the gene started out as inessential, contributing nothing? After the gene duplication occurs, both genes continue to be subject to mutation. Mutations in the second gene cannot transition it from inessential to essential. But mutations in the first gene can change the actions of the first player such that they can no longer solve the room on their own. As long as the second player can pick up the slack, this mutation in the first gene is “silent” or neutral with respect to fitness. As a result, it cannot be removed by negative selection. But it doesn’t really need to be; the team still does just fine and solves the room. In this way, a complex solution evolves from a simpler (single player) solution, without any positive selection that would favor complexity.

In biology, this pathway to complexity has been called constructive neutral evolution. It’s constructive because it is building or adding parts to a biological pathway. And it’s neutral because each of the steps has no impact on fitness. As I’ve noted before, our simulation doesn’t prove that constructive neutral evolution occurs in biology, but it does illustrate how it can happen in an accessible and visual way.

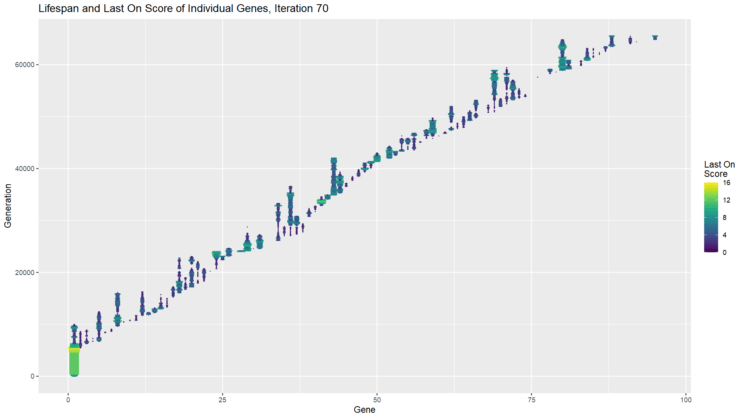
In fact, not only can constructive neutral evolution add parts to a solution, it can replace them. Check out the chart above. I’ve chosen a single iteration of my experiment, but this phenomenon happens every time. The vertical lines each represent a single gene, with the vertical position indicating at which generation the gene first appeared (bottom) and when it was lost (top). So the first gene naturally appears at generation 0 and is lost around generation 10,000; gene 1 appears around generation 5,000 and is lost around generation 8,000; and so on. The width and the color of the line represent the gene’s LOTB score at that generation. The first gene increases its LOTB score until it solves the room; at that point a second gene is added, and shortly thereafter the LOTB score of the first gene starts to go down, eventually reaching zero, after which time the gene is lost. From there, you can see multiple cycles of a gene being added, the LOTB of the other genes doing down, the LOTB score of the new gene going up, and then even more genes getting added while that gene’s LOTB score goes down again.

In biology, we would not necessarily expect to see this much turnover of genes. For one, 70,000 generations is a long time for many organisms. But more significantly, we are duplicating the same gene very often. Real organisms have tens of thousands of genes, and while a gene duplication event of some kind may occur fairly frequently, any given gene would only get duplicated very infrequently. So this model is a somewhat heightened or exaggerated version of constructive neutral evolution, but that heightening makes it easier to see and understand the relevant principles. Dynamism and volatility at the genome level is possible even if the phenotype or expression of that genome does not appear to change at all, at least with respect to fitness.

Now that I’ve pointed out a significant different between our model here and what happens biologically, it occurs to me that we could tweak the experiment slightly to get somewhat closer. (This is typical of the incremental work of science; critiquing the methods of one’s own work suggests further iterations and refinements. The intermediate steps might never been seen outside of the lab where they occur, but I want this to be more of a work-in-progress blog so you can see the process rather than just the results.) Using the same rates of addition and loss, we can replace the duplication step with the addition of a random gene. This would be more comparable to duplicating some other gene, rather than duplicating the gene for the solution. This makes it less likely that the added gene will be able to contribute materially right away. Will some of those added random genes become essential before they are lost? As before, you can try that out below or click here for a bigger version if needed. Let’s see what happens.