Two weeks ago, we revisited the Quandary Den to see what happens when multiple players are able to work together. We did this by modeling gene duplication, a known biological process. Last week we saw some results showing that solutions involving multiple players could evolve, and when multiple players got involved solutions tended to come faster. At the same time, more wasn’t always better; we saw that when players were added too quickly, they were more likely to get in the way and inhibit solutions. This little model gives us a picture for how organisms might evolve complexity, that is solutions involving distinct, coordinated parts. In this case, we have an adaptive pathway to complexity, since adding players provides opportunities to potentially increase fitness. But is that the only road to complexity?
We ended last week with the question of what happens if gene duplication–adding players–doesn’t start until a complete single-player solution has evolved. That would eliminate the possibility of an adaptive pathway to complexity, since additional players can’t increase fitness. Do you expect a complex solution to evolve under these conditions, or do you expect that the single player solution will persist against a background of irrelevant gene duplication and loss? If you expect a complex solution to emerge, do you think it will tend to have more parts or fewer or the same? You can experiment at the bottom of this post (or here if the embed below is inconvenient) and we’ll compare results next week. Feel free to share your hypotheses or predictions or results in the comments!
I showed you last week that through gene duplication, the number of genes increased over time. We compared those numbers and rates of increase to a duplication scenario without fitness implications and saw significant differences, implying that the added genes had something to do with the function of solving the room. If the added genes were unrelated to that function, we’d expect their numbers to follow the same patterns and trends as the random walk simulation. Still, that evidence is indirect; can we assess contributions more directly?
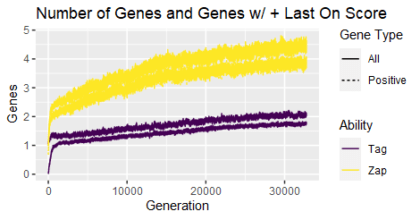
I propose we look at a metric called last-on-the-bus (LOTB) value. LOTB value comes from productivity assessments of work teams, with the idea of asking how much value a given team member adds if they are “last on the bus” or the last person added to the team. In other words, what’s the difference between the performance of the team of everyone except the given member and the performance of the team with everyone including them? We can assess that directly; just rerun the Quandary Den simulation with a genome missing a given gene (chromosome) and repeat for every gene. The difference between the whole team/genome score and the team minus one score is the LOTB value. The chart at the top of this post shows the total number of genes (solid lines / upper line of each color pair) and the number of genes with a positive LOTB value (dashed lines / lower line of each color pair). Those stats are shown for taggers (purple / darker lines) and zappers (yellow / lighter lines). A positive LOTB value indicates that the gene and the player whose actions it encodes are making a contribution to the overall team that does not overlap with others’ contributions; the full solution is not possible without the contribution of those players. Not every gene and player has a positive LOTB value, but over time the number of genes with positive LOTB values does increase, and with a comparable pattern to the overall number of genes.
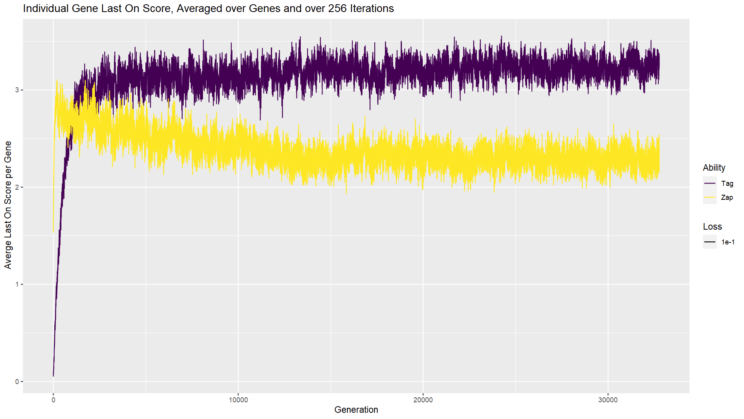
The chart above shows the average LOTB value per gene for taggers (purple / dark line) and zappers (yellow / light line). Keep in mind that in this scenario, the overall team fitness is also increasing, which is why the tagger LOTB value can increase even while the number of genes increases. Interestingly, the zapper LOTB increases, then decreases before appearing to level off. Since there tend to be more zappers, they have to divide up the total team value between more players than the tagger teams, leading to a lower average LOTB value per player. Overall though, we can conclude that what is evolving is genuinely complex in the way I described initially. Not only are there multiple players, but most players are making contributions that are not redundant with any other player’s contributions.
Next week we’ll look at LOTB values for the scenario you’ll be experimenting with, where the room is solved from the start. For your live results, I’ve plotted something slightly different. Since the best fitness will remain 16 through the experiment, plotting that isn’t interesting. So now the fitness chart will show the best solo fitness among all the genes in each generation. By solo fitness, I mean the fitness a given gene achieves when its player plays alone. At the beginning, there is just one gene and its player can already solve the room, so the value will be 16. If the best solo fitness ever drops below 16, that means no player can solve the room on their own and your players have started down a nonadaptive road to complexity.
Here’s your “lab” for this week (and again this is an option if the embed below doesn’t meet your needs),
Andy has worn many hats in his life. He knows this is a dreadfully clichéd notion, but since it is also literally true he uses it anyway. Among his current metaphorical hats: husband of one wife, father of two teenagers, reader of science fiction and science fact, enthusiast of contemporary symphonic music, and chief science officer. Previous metaphorical hats include: comp bio postdoc, molecular biology grad student, InterVarsity chapter president (that one came with a literal hat), music store clerk, house painter, and mosquito trapper. Among his more unique literal hats: British bobby, captain’s hats (of varying levels of authenticity) of several specific vessels, a deerstalker from 221B Baker St, and a railroad engineer’s cap. His monthly Science in Review is drawn from his weekly Science Corner posts — Wednesdays, 8am (Eastern) on the Emerging Scholars Network Blog. His book Faith across the Multiverse is available from Hendrickson.

Leave a Reply