For the past few weeks, we’ve been conducting experiments in the Quandary Den, a simple game simulation where the players evolve strategies. We’ve been looking at how complex solutions can evolve from simpler ones. So far, no single technical definition captures everything we mean informally by complexity, but for our purposes here I am describing a solution as more complex if it involves more distinct parts that are each individually essential. Last week we confirmed that there are neutral roads to such complexity, meaning the changes involved in going from a simpler solution to a more complex one do not change fitness and are not selected for. Nevertheless, even though we are not selecting for higher complexity either directly or indirectly, complexity always increases in these experiments. Then I identified a way in which I might have inadvertently made greater complexity more likely, and proposed a modification to our experimental setup that would mitigate that potential bias. Did the road still lead to more complex solutions? What did you find? Let’s look at my results.
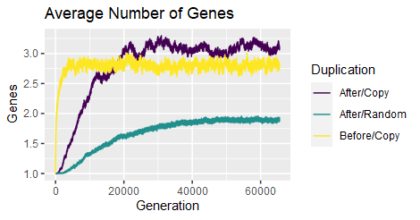
We are comparing three scenarios. In all scenarios we start with a single player who is a zapper with a 128 base-pair gene, initialized randomly; over many generations, we introduce mutations and keep those that don’t decrease the player’s score in our game. In the first scenario (yellow/lightest line), gene duplication occurs from the beginning so that fitness/score improvements can come from mutating existing genes or adding a new gene; we called that the adaptive road to complexity. In the second scenario (purple/darkest line), gene duplication only occurs after a single player has evolved to find a complete solution alone; we called this a neutral road to complexity. In the third, new scenario (green/intermediate line), we still require a single player to find a complete solution first, then we add occasionally add random genes rather than duplicating existing genes. This is potentially another neutral road to complexity, modeling either de novo gene creation or duplication of some other hypothetical gene unrelated to solving this Quandary Den puzzle (the latter is more common in biological scenarios).
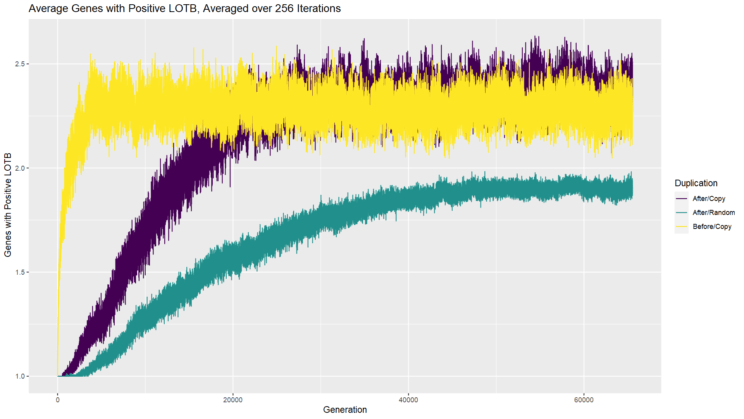
We can see that complexity increases in the first two scenarios by looking at the number of genes overall (chart at the top of the post) and see that it increases, by looking at the number of genes with a positive last-on-the-bus (LOTB) contribution (chart above) and see that it increases as well, and by looking at the average LOTB contribution (chart below) and see that it decreases once a full solution has been found. And now we can see that the same trends occur in our third scenario as well, albeit with different equilibria. Even when the added gene starts out by making a random contribution rather than being a copy of a full solution, over time it becomes an essential contributor.
(Recall that the LOTB contribution is the difference between the full team score and the score of the team missing the single player whose contribution we are measuring. Any player with a positive LOTB contribution is essential in the sense that the team cannot complete a full solution without them.)
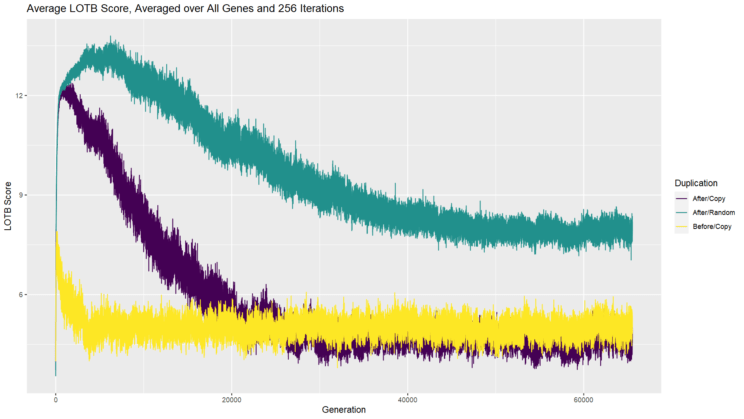
I think it is also interesting to note that in each scenario, an equilibrium is reached in terms of number of genes and average LOTB contribution. We might imagine that genes could be added indefinitely, or at least until the points are divvied up so each gene has an LOTB contribution of 1, the smallest positive option. But the number of genes (averaged across multiple iterations) levels off much sooner than that. This is possibly because the equilibrium value represents the point at which adding another gene is equally likely to detract from fitness (by zapping teammates or getting in the way of critical laser beams of teammates or just getting zapped by a robot) as not. Can you think of a way we could test this?
And with that, I think our exploration of the roads to complexity will take a break. Hopefully you’ve learned something about evolutionary processes and/or how scientists approach the challenges of finding questions to ask and answers to those questions. Let me know in the comments if there’s anything you’d like to clarify or expand on, or if you have research questions of your own you’d to investigate in the Quandary Den.
Andy has worn many hats in his life. He knows this is a dreadfully clichéd notion, but since it is also literally true he uses it anyway. Among his current metaphorical hats: husband of one wife, father of two teenagers, reader of science fiction and science fact, enthusiast of contemporary symphonic music, and chief science officer. Previous metaphorical hats include: comp bio postdoc, molecular biology grad student, InterVarsity chapter president (that one came with a literal hat), music store clerk, house painter, and mosquito trapper. Among his more unique literal hats: British bobby, captain’s hats (of varying levels of authenticity) of several specific vessels, a deerstalker from 221B Baker St, and a railroad engineer’s cap. His monthly Science in Review is drawn from his weekly Science Corner posts — Wednesdays, 8am (Eastern) on the Emerging Scholars Network Blog. His book Faith across the Multiverse is available from Hendrickson.

Leave a Reply