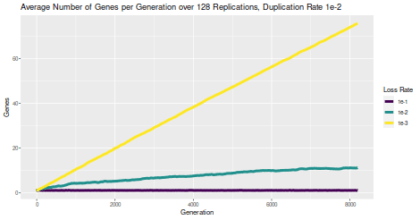
Last week, we talked about gene duplication and looked at some simulation results. For starters, I was just simulating a random walk in the number of genes. The probability of adding a gene (taking a step ‘up’) remained the same, but I varied the probability of losing a gene (taking a step ‘down’). And I prevented the number from ever getting to zero or lower. You can see the results to the right (click for a bigger version). When the probability of losing a gene is 10x higher than gaining (purple/darkest line), the number of genes (averaged over 128 trials) basically stays at 1. No big surprise there; any time a gene is gained, we’d expect to lose it again very quickly before another one is added. Conversely, when the probability of losing a gene is 10x lower than gaining (yellow/lightest line), the average number of genes just keeps on growing; again, not a big surprise. But when the probability of gaining and losing a gene is the same (green/intermediate line), the average number of genes creeps up, possibly leveling off somewhere just above 10. You’d probably expect some kind of equilibrium, but would you have predicted that’s where it would be?
I also gave you a chance to see what happens when we introduce gene duplication to the Quandary Den simulation. The gene duplication process is the same, except that now fitness and selection come into play. If a gene duplication or loss has a negative impact on fitness, that genome is not retained and the ‘parent’ genome undergoes mutation and duplication/loss again. If gene duplication or loss has a neutral or positive impact on fitness, that genome is retained and undergoes further mutation and possible duplication or loss. What happens when we let our players bring friends? First, let’s look at the number of genes in the chart below.
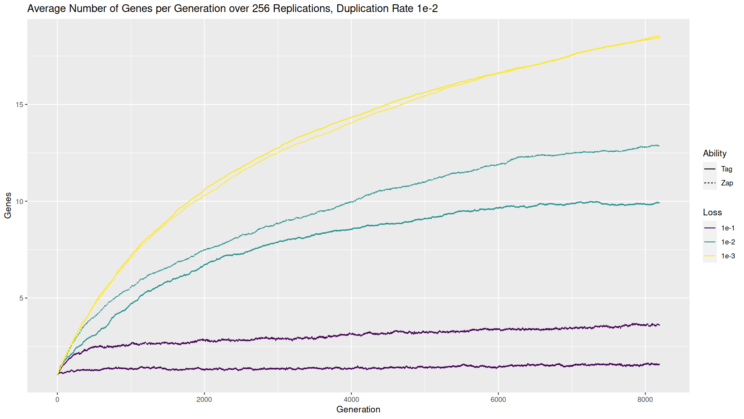
I’ve plotted the average number of genes again, for the three loss rates as before, for zappers (dashed lines; if you can’t distinguish, the dashed line is higher for the 1e-1 and 1e-2 loss rates and lower for the 1e-3 loss rate) and taggers (solid lines). Most notably, even when the loss rate is 10x smaller than the duplication rate (yellow/lightest line) the number of genes does not grow in an unbounded fashion. Conversely, when the loss rate is 10x greater than the duplication rate, the zappers manage to accumulate multiple genes which is more than was seen in the random walk; the taggers stay around 1 gene. For the balanced scenario, the equilibrium is about the same as the random walk, possibly somewhat higher for the zappers.
These results in terms of gene number suggest multiple effects when fitness becomes part of the equation. On the one hand, when loss is more likely or equally likely to duplication, having multiple zappers can make it easier to increase fitness, making it more likely for genes to accumulate. On the other hand, when duplication is more likely, the proliferation of players creates more opportunities for players on the same team to tag or zap each other, which limits the accumulation of genes in that scenario.
We can also take a look at fitness directly; what happens there? Below is the chart of fitness. Keep in mind that this fitness of the genome generated at every generation, regardless of whether it is retained for further replication or not. And the results are averaged across 256 iterations. I’ve also included for comparison the scenario with no gene duplication or loss, so just one player at all times.
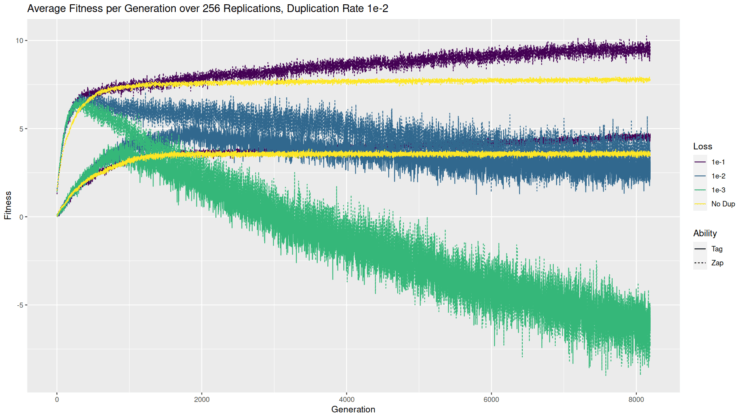
As we’ve seen before, zappers (dashed lines) generally do better than taggers (solid lines), all else being equal. And as we might expect, including multiple players through gene duplication provides an early fitness advantage over a single player (yellow/lightest lines). But the single player catches up quickly. And then the really interesting bit happens. When duplication is equally or more likely than loss (blue & green/intermediate lines), the average fitness starts to decline after a while. That does not happen when loss is more likely than duplication (purple/darkest lines), where the average fitness continues to increase, albeit slowly.
I think the way to understand this is to think about the interaction of duplication and mutation. A duplicate gene will add a player, but that player will make exactly the same moves and so its opportunity to contribute to the fitness is minimal. Over time, mutations may allow it to make different moves and make a contribution, or to make different moves and tag or zap other players. If genes are added slowly, there is time for the new gene to mutate a positive fitness contribution before another gene is added. Whereas if genes are added quickly, they have more opportunities to interfere with each other than to contribute. They also have the chance for an even lower overall fitness, because total tags or zaps to players are subtracted from the tags or zaps they score on the robots; more players means more can potentially be subtracted. This impact of adding players has some analogue in biology, where gene dosing is important to function and fitness; duplicating a gene can double its dose, which may be useful or detrimental. Now, I don’t think we can infer much about biology from these simulations, especially with respect to specific rates or equilibria. That’s not the point of these simulations; rather, the point is to illustrate phenomena that we already know occur in biology.
Having experimented some with gene duplication in the context of evolving fitness, that is while the players are still trying to solve the room, next week we’ll move on to scenarios where duplication occurs after an initial player has already solved the room. What do you suppose will happen then?
Andy has worn many hats in his life. He knows this is a dreadfully clichéd notion, but since it is also literally true he uses it anyway. Among his current metaphorical hats: husband of one wife, father of two teenagers, reader of science fiction and science fact, enthusiast of contemporary symphonic music, and chief science officer. Previous metaphorical hats include: comp bio postdoc, molecular biology grad student, InterVarsity chapter president (that one came with a literal hat), music store clerk, house painter, and mosquito trapper. Among his more unique literal hats: British bobby, captain’s hats (of varying levels of authenticity) of several specific vessels, a deerstalker from 221B Baker St, and a railroad engineer’s cap. His monthly Science in Review is drawn from his weekly Science Corner posts — Wednesdays, 8am (Eastern) on the Emerging Scholars Network Blog. His book Faith across the Multiverse is available from Hendrickson.

Leave a Reply