Mathematical models of the spread of infectious diseases are a big reason I have the job I have now. When I first encountered them in grad school, a whole new world of scientific possibilities opened up. Suddenly there was an overlap between my math & computer skills and the biology which fascinated me. As it became apparent that my laboratory skills were lacking, it was a relief to know I could still contribute to improving public health with the skills I did have. Seeing the various applications and extensions of those models deployed for the present COVID-19 pandemic has renewed my enthusiasm, even as they also provide some reassurance that there is an order to what we are experiencing now, however partially we may understand it. Particularly intriguing was work on a clustering parameter, both because it is new (to me) math and because it offers some hope for better control of the coronavirus.
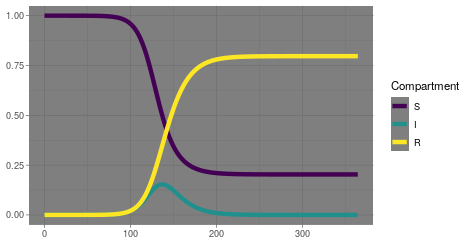
Epidemic models have nearly a century of history of research behind them. It all started with a variation of what we now call the SIR model, named for the three compartments people can occupy: Susceptible, Infectious and Recovered (or Resolved). The model starts with a population of people who are susceptible to the disease and one or more people who are infectious. Then it assumes all those people mix at random, and over time the infectious people interact with the susceptible people and consequently infect them. Those infectious people can spread to still others, until their infection resolves and they can no longer infect or be infected. Classically, these people, events and interactions are not simulated individually but by a trio of differential equations with parameters representing the rates at which the events occur. As such, the model is a gross oversimplification, and over the past century many variations have been developed to more closely represent reality. Recently, computational capacity has reached the point that some researchers actually do now simulate an entire country’s worth of people individually, down to specifying family units and coworkers and other interpersonal connections which facilitate the spread of infection.
But even the simple SIR model offers significant insights. From that model we get the concept of R0 or the basic reproductive number. For the system of three differential equations, you can demonstrate analytically that R0 represents the number of people that will get infected if you introduce a single infectious person into an otherwise fully susceptible population. If it is greater than 1, infections will spread and increase exponentially, as we have seen. But for a fixed population size, that growth can only persist so long before there are not enough susceptible people to infect. Eventually, growth in cases will slow and then level off and then decrease until there are no infectious people. Notably, this can happen before every susceptible person has been exposed and infected, leading to the concept of herd immunity. The exact balance of recovered people and remaining susceptible people when this occurs depends on the exact value of R0. The bigger R0 is, meaning the infection is more easily spread, the more people need to be recovered to achieve herd immunity. That’s why when vaccine acceptance goes down, we see measles outbreaks; the R0 for measles is quite high and requires nearly everyone in the population to be immune for herd immunity.
For the coronavirus we currently face, R0 seems to be around 2 or 3, although it can be challenging to estimate. Because the math is simple, R0 has to average over many different features of the infectious process, including the biology of the virus, the biology of people, and the behavior of people. So R0 is not purely an intrinsic property of the virus. This brings us to the recent research on adding a second parameter, k. Basically, instead of having a single R0 that averages of all those factors, every person has their own R. Those individuals Rs follow a distribution, reflecting the contributions from the virus’s biology and the commonalities of human biology, while also allowing for some individual differences in biology and behavior. The larger k is, the more similar everyone’s R value; conversely, if k is closer to 0, the different Rs are more varied, meaning some people will tend to spread the virus more than others. There is evidence that this coronavirus spreads via a wider range of scenarios, some with lots of transmission and some with very little. That range is typical of a smaller k value, an observation borne out by some numerical estimates of the parameter. That is encouraging for control efforts in general, although it may make returning to large scale events that much more challenging.
InterVarsity President Tom Lin shared the following response to the current tensions in the United States. I would recommend giving it a read. I’d also recommend checking out the following conversation on science related to race when it goes live next Monday (6/8) at 3pm Eastern.
Andy has worn many hats in his life. He knows this is a dreadfully clichéd notion, but since it is also literally true he uses it anyway. Among his current metaphorical hats: husband of one wife, father of two teenagers, reader of science fiction and science fact, enthusiast of contemporary symphonic music, and chief science officer. Previous metaphorical hats include: comp bio postdoc, molecular biology grad student, InterVarsity chapter president (that one came with a literal hat), music store clerk, house painter, and mosquito trapper. Among his more unique literal hats: British bobby, captain’s hats (of varying levels of authenticity) of several specific vessels, a deerstalker from 221B Baker St, and a railroad engineer’s cap. His monthly Science in Review is drawn from his weekly Science Corner posts — Wednesdays, 8am (Eastern) on the Emerging Scholars Network Blog. His book Faith across the Multiverse is available from Hendrickson.

Washington post had a simulation of the SIR model that shows it well: https://www.washingtonpost.com/graphics/2020/world/corona-simulator/?itid=hp_hp-banner-low_virus-simulator520pm%253Ahomepage%252Fstory-ans
Understanding of this issue is quite necessary. We have to be aware of what it is and how we have to fight against that!